[10000印刷√] 面積 比 公式 218472
円の面積の求め方 円の面積を求めるときは 円の面積 = 半径 × 半径 × 円周率 という公式を使います。 たとえば、半径が 3 c m の円の面積は 半径 半径 円周率 半 径 × 半 径 × 円 周 率 = 3 × 3 × 314 = 26 c m 2 と求めることができます。
面積 比 公式- 面積比は2乗してやった比の、 1² 2² = 1 4 になるはず! おめでとう! 相似比から面積比を計算できちゃったね。 面積比の公式をつかった問題に挑戦! 面積比の公式でもう1つ問題を解いてみよう。 公式はつかっておぼえるのが一番!円の面積を求める公式は、次の通りです。 円の面積 = 半径× 半径×314 円の面積 = 半径 × 半径 × 314 中学生以上では、文字を使って次のように書きます。 S = πr2 S = π r 2 半径 r の円 ここで、S は円の面積、π は円周率、r は円の半径を表します。 この
面積 比 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  | |
 |  |  |
「面積 比 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
 |  |  |
「面積 比 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 | ||
「面積 比 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「面積 比 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「面積 比 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 | ||
「面積 比 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「面積 比 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
 | ||
「面積 比 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |
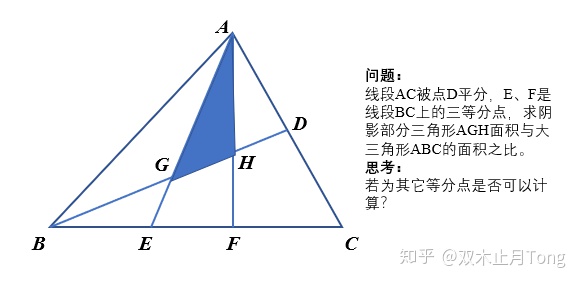
さらに、相似比が1:3であれば、三角形の底辺も高さも3倍になるので面積比は1:9になります。 このことから、多角形について ということが分かります。 相似比から面積比を求める考え方はよく使うので、しっかり理解しておきましょう。 三角形の相似 あとは面積比を考えればおしまいですね。辺の比が分かっているので、面積比も求めることができます。 三角形 ABC の面積を S とすると、 $\mathrm{ BD }\mathrm{ DC }=54$ なので、三角形 ABD の面積は $\dfrac{5}{9}S$ 、三角形 ACD の面積は $\dfrac{4}{9}S$ となります。
コメント
コメントを投稿